问题)夏普比(Sharp Ratio)是什么?
- 投资收益率超过无风险收益率的概率。
- 如果夏普比越大的话,该投资的收益率超过无风险收益率的可能性也就越大。
- SR=(x-bar – Rf) / s *x-bar : x平均值, Rf : Risk Free,一般来说债券的利益率, s : 标准差
- r~N( µ, σ二乗 )
问题)如何计算初始金额为A的投资的VaR?
- 假设收益率x是正态分布,满足x~N(µ,σ2乗)
- 则z=(x- µ)/ σ服从标准正态分布,即z ~N(0,1)
- 99%VaR,则α=0.01。
- 99%VaR = A*P1=A*(µ – 2.33*σ)
问题)在正态分布下,SPAN的值是什么?
- SPAN=P95-P5; σ=0.05。
- P95=µ+σ*1.64, P5=µ-σ*1.64
- SPAN=(µ+σ*1.64) – (µ-σ*1.64) = 3.28*σ
问题)正态分布的额特点是什么?
- 落在距离均值1倍的标准差内的概率是0.68。
- 落在距离均值1.96倍的标准差内的概率是0.95
- 落在距离均值2倍的标准差内的概率是0.993
- 落在距离均值3倍的标准差内的概率是0.997
问题)中心極限定理是什么?
- 不管总体的分布是什么形态,如果它的期望值或者平均值是μ,方差是σ平方,只要样本的容量n非常大,样本的平均值总是近似服从正态分布。
- 標本を抽出する母集団が平均µ、分散σの二乗の正規分布に従っていても、なくても、抽出するサンプルサイズが大きくなるにつれて、標本平均の分布は、平均µ、分散σ二乗/nの正規分布N(μ, σ二乗/n )に近づく。
问题)置信区间(Confidence Interval)的含义是什么?
- 该区间被称为总体均值的95%的置信区间,95%是置信度或置信水平。
- 抽取100个样本,计算出100个样本的平均值和100个样本的区间,那么,它们当中至少应该有(1-α),因此,可以以( 1-α )的置信度(把握)相信µ落在一个这样的区间里面。
问题) t分布和正态分布的区别是什么?
- t分布与正态分布形状相像,但是峰值比正态分布低,尾部比正态分布厚,所以对于相同的置信区间。
- 正态分布比t分布的置信水平更高,而在相同的置信水平下,t分布的置信区间相比正态分布更大。
- t分布的自由度越高,越接近标准正态分布。
问题)什么时候才需要用到 t 分布?
- 对于n小于30的情况,即小样本的时候,样本均值的抽样分布不能用正态分布来近似,此时需要用t分布去近似。
问题)自由度是什么?
问题)“假设检验”是什么?
问题)第一类错误和第二类错误的差异是什么?
- 第一类错误:H0是真的,但是你选择H1。
- 第二类错误:H0是假的,但是你选择H0。
问题)Neymann-Pearson原则是什么?
- 不可能找到一个两类错误都不犯的检验。
- 二つの間違いのいずれかを探すことができないことは、間違いを犯すことがないという検定。
问题)P-值是什么?
- 原假设成立时,你能够观测到如此极端的样本的概率。犯第一类错误的概率。
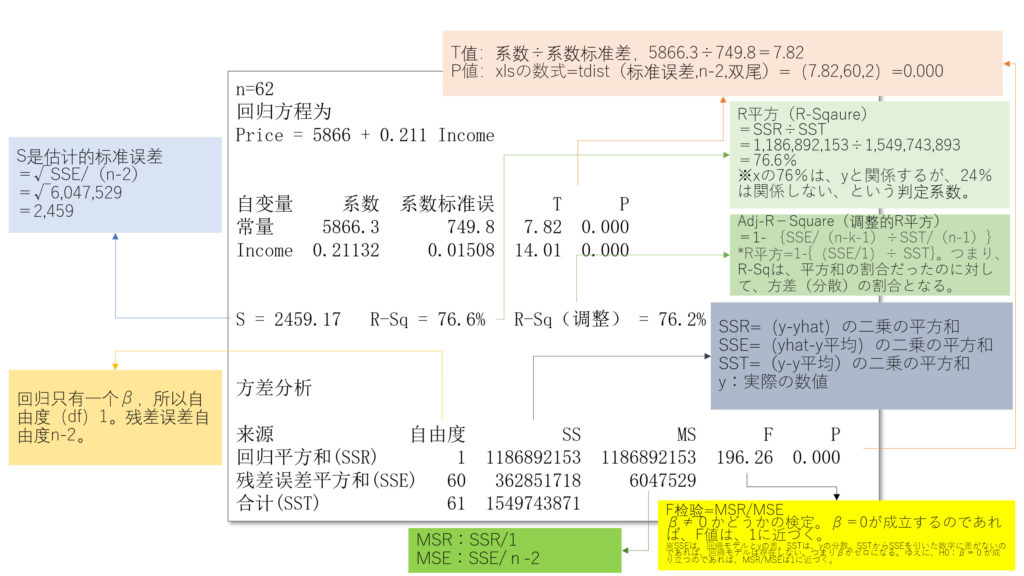
问题)F检验是什么?
- 检验变量X对Y有没有解释作用。F的值足够的时候拒绝原假设H0。F值=(SSR/1)÷(SSE/n-2)
问题)最小二乘法是很么?什么时候用它?
- 检验x和y的关系的函数正确不正确的方法。2つのセットのデータの組(x、y)がn個与えられた状況で、xとyに直線的な関係があると推察できるときに、もっともと相応しい直線を求めるための方法。
问题) 异方差(分散不均一性,Heteroskedasticity)是什么?
- 回归model(y-hat)和实际值(y)的残差越来越离开的情况
问题)资产定价模型(CAPM)是什么?
- Capital Asset Pricing Managemen
问题)虚拟变量(Dummny Variable)是什么?
- これは、数字を持たない男女、季節などを因数として組み込む時に使う。例えば、男:0、女:1と設定する。
问题)R-Square(R平方)=100%是最好的model吗?
问题)公式
- 样本比率的抽样分布:p-bar~N(p, p(1-p)/n )
- SE(p-bar)=√p(1-p)/n