テーマ「简单线性回归模型(単回帰モデル)のつづきと回归模型的预测与诊断」
- 前回は、単回帰モデルで、R平方(R-Square)により、β-hatとy-hatとの相関性を検証できるということを習った。今回は、その続き。
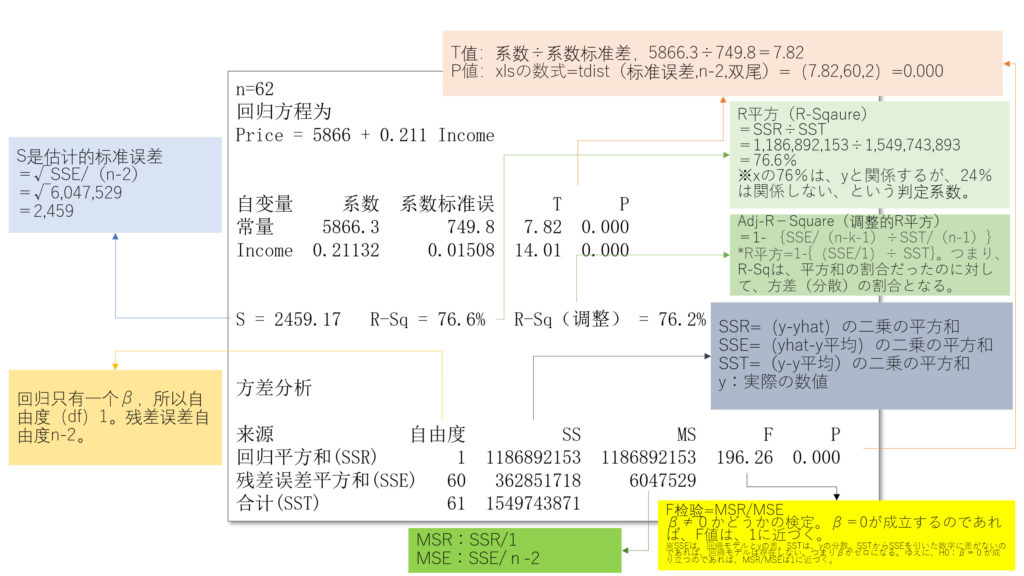
- F检验(F検定)はy=α+β・x+eとした回帰モデルがあるときに、変数Xとyの関係性を検証するもの。H0:関係性がない H1:関係性がある、とした時のF統計量は下記の通り。
- F=(SSR÷1)÷{SSE÷(n-2)}、F値が大きくなればなるほど、H0を拒否できる。 ※SSR(Sum of Squard Residuals)=回归平方和、SSE(Sum of Squared Errors of Prediction)=残差平方和
- 補足、MSR=SSR÷1、MSE=SSE÷(n-2)と呼ぶ。Mはmeanで平均のこと。詳細は下記図の通り。
- SSEは、回帰モデルとの差であるから、SSEが大きい=回帰モデルとの乖離が大きい場合は、F値は、小さくなり、H0を拒否できない。F値が大きいということは、SSEが小さい=回帰モデルとの乖離が少ないということで、H0を拒否できる。
- ExcelでのF分布の確率や数値を出すことが可能。確率Prob=fdix(x,df1,df2)X=finv(prob,df1,df2)。このdf1は、SSTの自由度、df2はSSRの自由度。
- minitabを使ったF値の算出方法は下記動画1)参照。また、単回帰モデルを出す式(最小二乘方法)はexcelで求められる。詳細はコチラ
- 资本资产定价模型(CAPM=Capital Asset Pricing Model)。回帰モデルで投資の組み合わせでリスクを管理するのが、CAPM。
- minitabを使って、Armandのピザの事例を使って、残差0を基準にして、拟合值(y-hat)と残差の関係を表す残差図を出してみる。(下記参照)残差0に近いほど、回帰モデルに近いことを表す。今回算出した分散図をみると、特別な規則はなく、ランダムで数字がならんでいる。動画2)参照
- さらに、yとxに、xの2乗も含めた二次曲線回帰の数値を調べてみる。
- ちなみに、この二次曲線回帰は、残差图が二次曲線になっている場合の回帰モデル化のために使う。
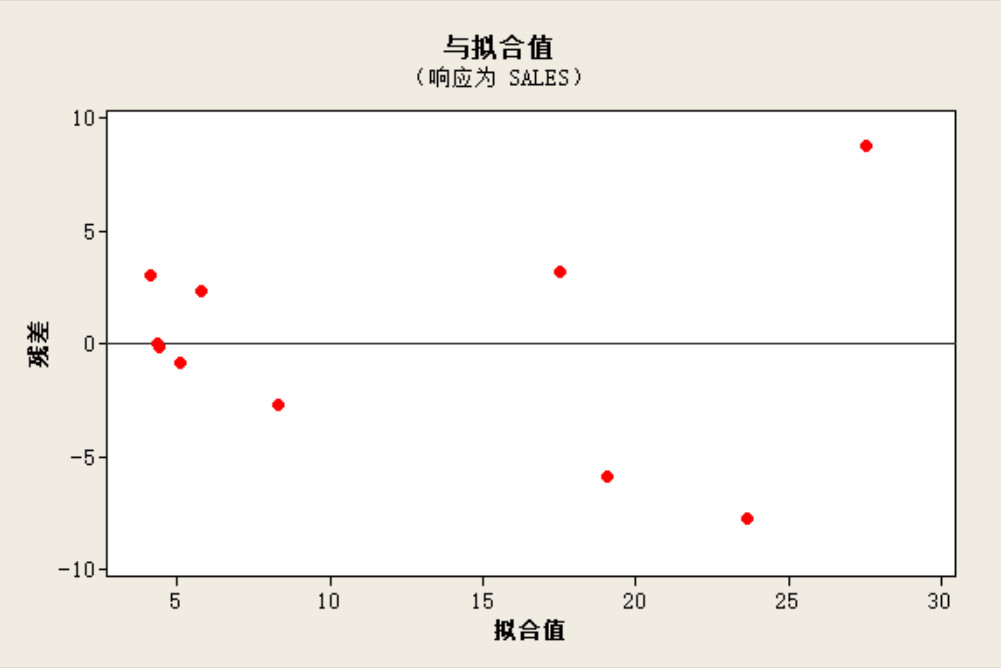
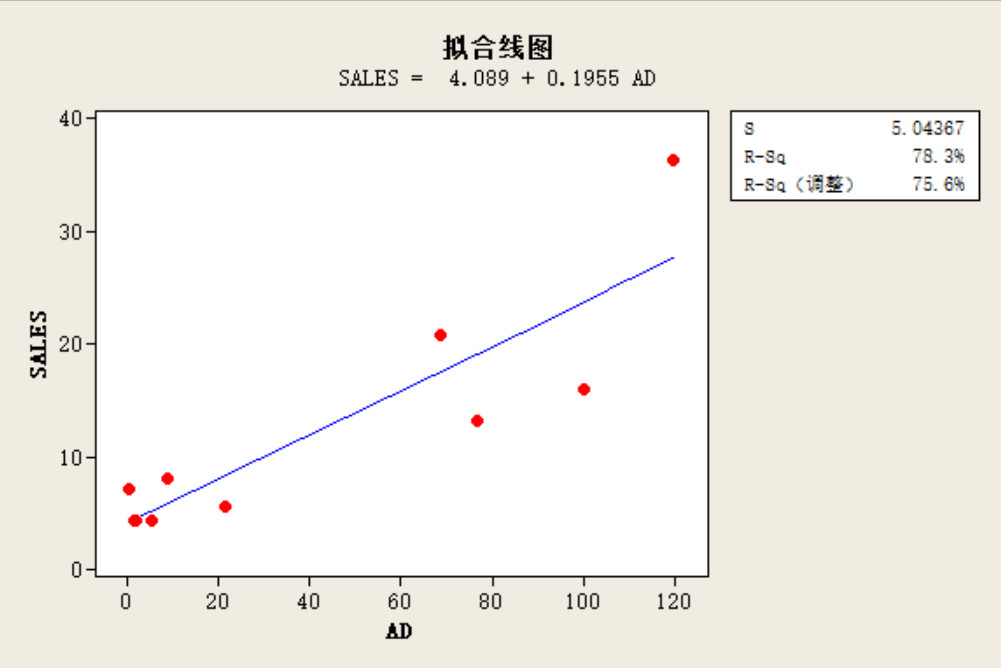
- 今度は、またminitabを使って、広告と売上の相関を調べてみる(事例Superbrands)。同様に、残差图を出してみると、拟合值(y-hat)の数値が大きくなればなるほど、残差が大きくなり、0と離れていく(散开)。画像2)3)参照。
- この乖離のことを、异方差(分散不均一性)、英語では、Heteroskedasticityという。つまり、単回帰のモデルが成立していないということ。
- これは、例えば、収入と消費額の関係を見ればわかりやすい。収入と消費額の単回帰モデルが成立するのか?いや、成立しない、収入が増えれば、消費額が増え続けるかといえばそうではない。ある人は、収入と比例して消費額が増えるかもしれないが、ほとんどの人は、比例して増えない。収入が増えれば増えるほど、消費額と乖離が出てくるのだ。
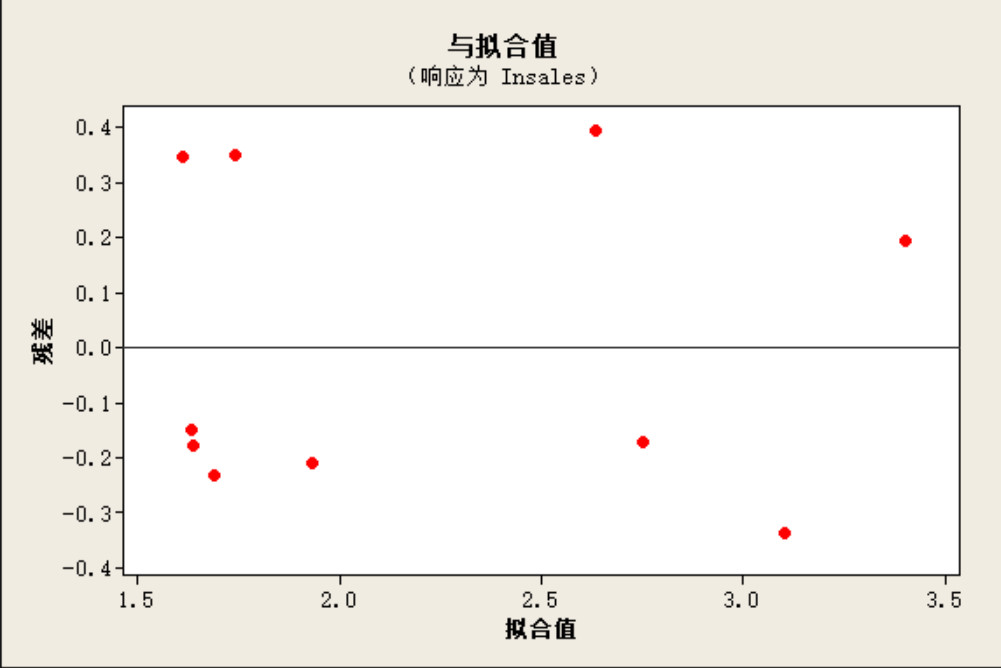
- この异方差があるときに、log変換をする。minitabでは、コマンド>let 列名loge(xの列名)で行える。log変換した後の値をyとして、x(AD)との関係を出すと、残差に対して平行となる。画像4)
- では、回帰モデルがどのように変わったのか?log変更前は、SALES(y-hat) = 4.09 + 0.196 AD、変更後は、Insales(y-hat) = 1.61 + 0.0149 AD。ADの変数を見ると、0.196から0.0149へ下がった。つまり、変更前は、ADが1増えると、SALESが0.196=約20%上がるというモデルだったが、変更後は、ADが1増えても、SALSは、0.0149=0.5%しから上がらないということ。
- 最後に広告と売上の別事例。回归→二次曲线回归→对数回归を検証。下記動画4)参照
今回は、minitabを使って、色々と検証をしましたので、わすれないように、自分でも動画をつくって、振り返りができるようにしました。二次曲線回帰、log回帰などの計算式は授業では、飛ばして、検証方法を説明していました。まあ、細かい計算式は、今後も使うことがないので、いいかなと。考え方、検証方法をしっかり頭の中に入れておきたいと思います。